06-23 08:36
벤치마킹
Notice
Recent Posts
Recent Comments
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 에어아시아
- 양양솔비치아침
- DFS
- 푸르지오포레피스
- 편도수술
- 아이혼자다녀옴
- 검색완료
- 당근마켓중고차
- 파이썬
- 종이캐리어
- 양양솔비치 뷔페
- 가족소고기외식
- 고마워다음
- 커피쏟음
- 사진에서 글자추출
- 양양솔비치조식
- 싱가폴중학교수학문제
- 영통역소고기
- 결항전문
- 중학교입학수학문제
- 사진문자추출하기
- 주차넉넉
- 영통외식
- 양양솔비치세프스키친
- 커피
- 홍시스무디
- 결항
- 오트눈썰매장
- 사진문자추출
- 영통칠프로칠백식당
Archives
- Today
- Total
너와나의 관심사
sklearn.metric 에서 함수들 본문
1. MAE (Mean Absolute Error)
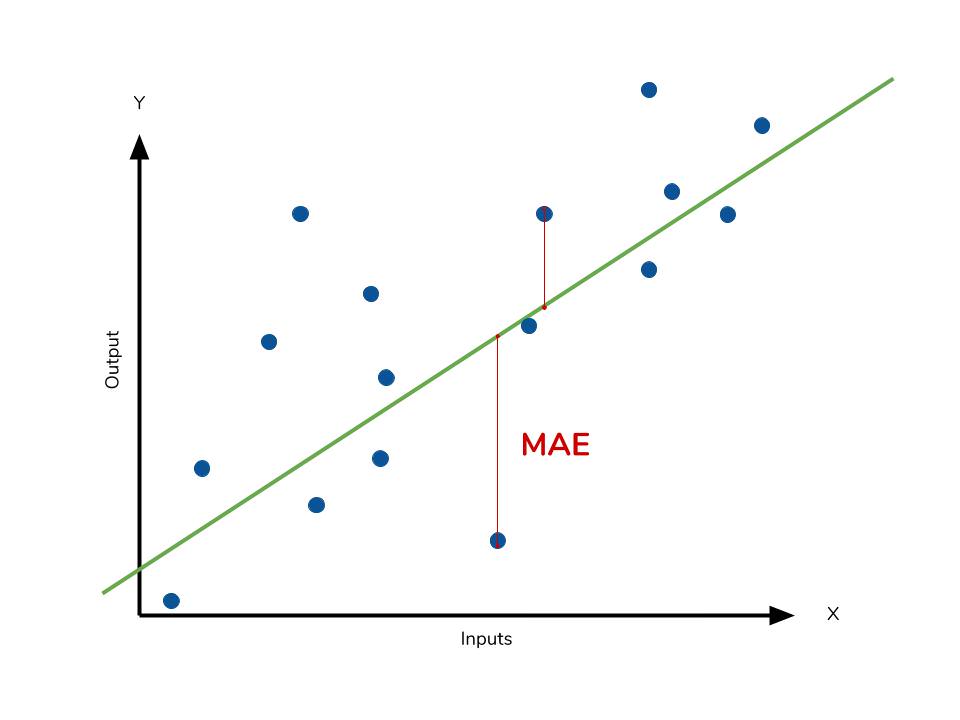
- 실제 값과 예측 값의 차이(Error)를 절대값으로 변환해 평균화
- MAE는 에러에 절대값을 취하기 때문에 에러의 크기 그대로 반영된다. 그러므로 예측 결과물의 에러가 10이 나온 것이 5로 나온 것보다 2배가 나쁜 도메인에서 쓰기 적합한 산식이다.
- 에러에 따른 손실이 선형적으로 올라갈 때 적합하다.
- 이상치가 많을 때
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
2. MSE (Mean Squared Error)
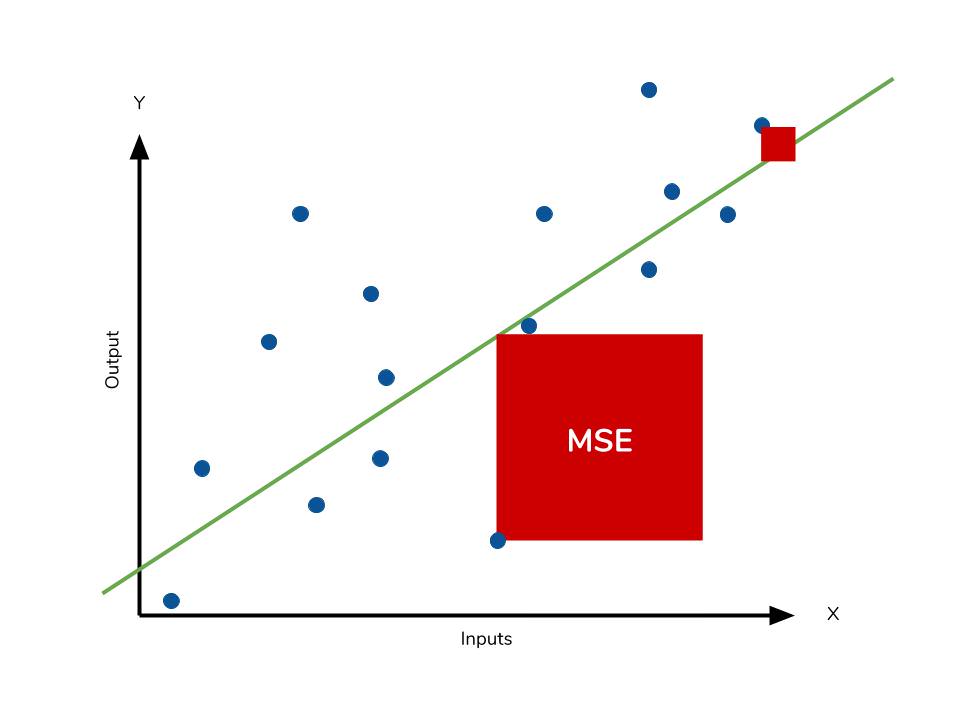
- 실제 값과 예측 값의 차이를 제곱해 평균화
- 예측값과 실제값 차이의 면적의 합
- 특이값이 존재하면 수치가 많이 늘어난다.
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)
3. RMSE (Root Mean Squared Error)
- MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있어 MSE에 루트를 씌운 RMSE 값을 쓴다.
- 에러에 제곱을 하기 때문에 에러가 크면 클수록 그에 따른 가중치가 높이 반영된다. 그러므로 예측 결과물의 에러가 10이 나온 것이 5로 나온 것보다, 정확히 2^2(4)배가 나쁜 도메인에서 쓰기 적합한 산식이다.
- 에러에 따른 손실이 기하 급수적으로 올라가는 상황에서 쓰기 적합하다.
from sklearn.metrics import mean_squared_error
MSE = mean_squared_error(y_test, y_pred)
np.sqrt(MSE)
4. MSLE (Mean Squared Log Error)
- MSE에 로그를 적용해준 지표
from sklearn.metrics import mean_squared_log_error
mean_squared_log_error(y_test, y_pred)
5. MAPE (Mean Absolute Percentage Error)
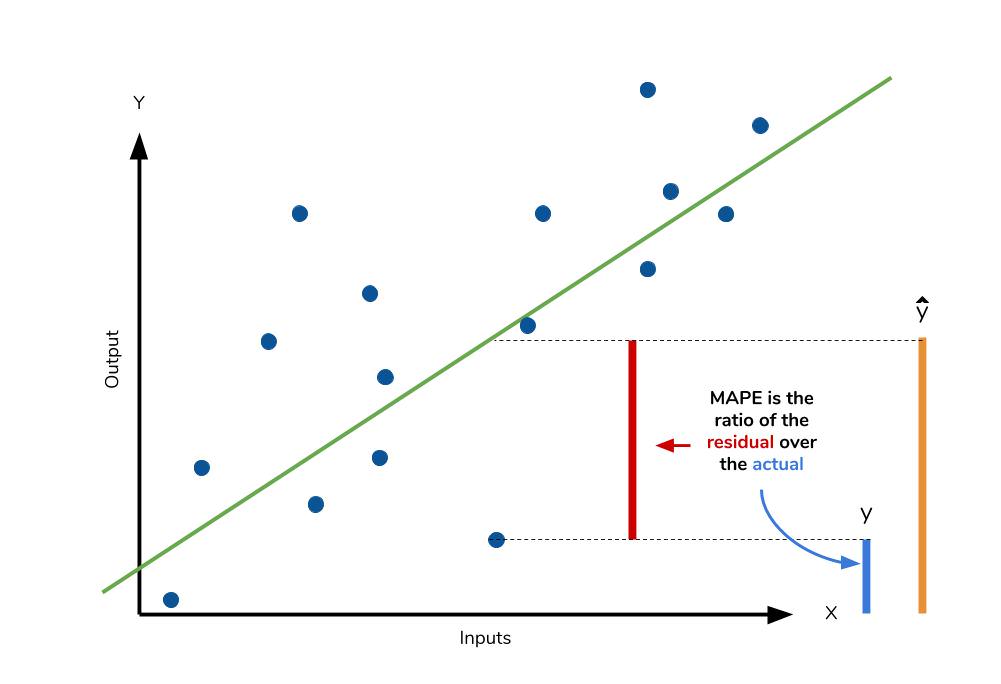
- MAE를 퍼센트로 변환
- MAE와 같은 단점
- 모델에 대한 편향이 존재
def MAPE(y_test, y_pred):
return np.mean(np.abs((y_test - y_pred) / y_test)) * 100
MAPE(y_test, y_pred)
6. MPE (Mean Percentage Error)
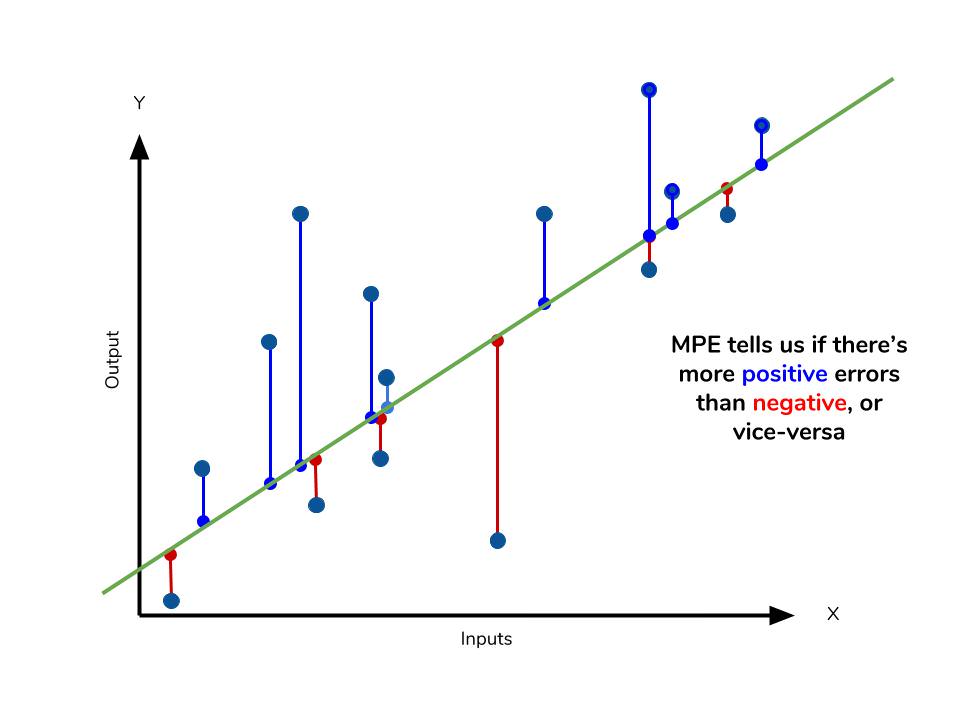
- MAPE에서 절대값을 제외한 지표
- 모델이 underperformance(+) 인지 overperformance(-) 인지 판단
def MAE(y_test, y_pred):
return np.mean((y_test - y_pred) / y_test) * 100)
MAE(y_test, y_pred)
Comments
