Densing law of LLMS paper

https://arxiv.org/pdf/2412.04315v1

이제는 num of parmeters 가 아니라 densing of LLM 밀도이다 

아래 그림은 chatGPT 출시 이후 밀도가 현재하게 높아짐을 보여준다 

계산 방법

 

 

 

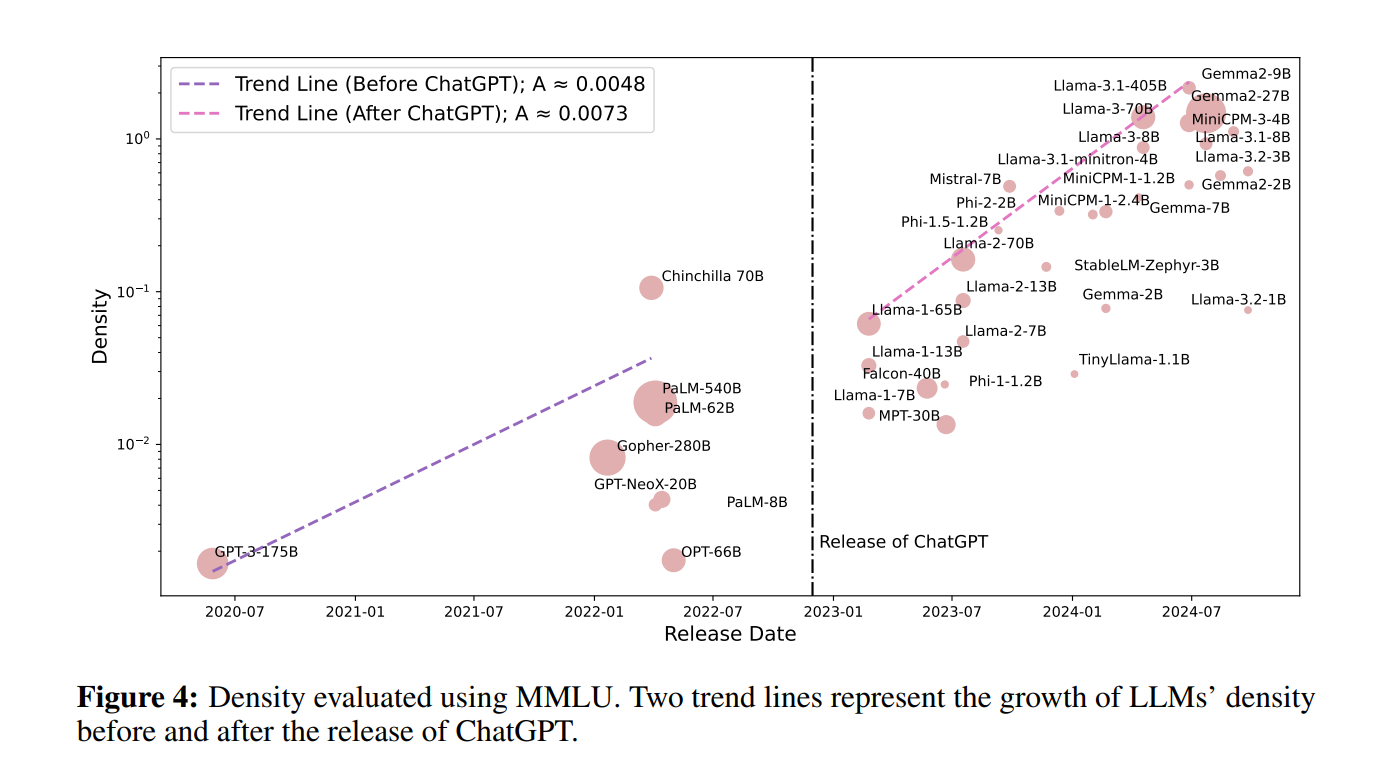
논문의 저자는

Gemma2 9B 만 이전 대비 capacity density 가 높아졌고 이에 반해

최신 llama3.2 1B, 3B 모델의 capacity density 가 낮은 이유로 training 완성도가 떨어져서  llama3.1 8B 보다 학습밀도가 떨어진것으로 보고있다. 이는 task 를 정의하고 충분히 학습한다면 유사한 capasity density 로 따라갈것으로 보고 있다.

 

 

대규모 언어 모델의 밀도화 법칙: 능력 밀도 개념을 중심으로

최근 대규모 언어 모델(LLM)의 발전은 모델 규모 확장에 따른 성능 향상에 크게 의존해왔습니다. 그러나 이와 동시에 계산 자원 소비 증가와 환경 배포의 비효율성 문제가 대두되면서, 모델의 "능력 밀도(capacity density)"를 새로운 평가 지표로 삼아 효율성과 성능 간의 균형을 모색하는 연구가 주목받고 있습니다. 2024년 12월 공개된 「Densing Law of LLMs」 논문은 이 개념을 체계화하며, LLM 기술의 지속 가능한 발전 방향을 제시합니다.

연구 배경

모델 확장의 한계

기존 LLM 개발 패러다임은 단순한 모델 크기 증가(파라미터 수 확장)에 초점을 맞추었습니다. 2020년대 초 GPT-3(175B)에서 시작해 2024년 기준 1조 파라미터 급 모델까지 등장하며 성능은 비약적으로 향상되었으나, 이는 에너지 소비량 증가(예: GPT-4 추론 시 50kWh/백만 토큰) 와 하드웨어 요구 사항 상승을 수반했습니다. 특히 에지 디바이스(스마트폰, 개인용 컴퓨터) 배포 시 모델 경량화 압력이 급증하며 효율성 연구의 필요성이 대두되었습니다.

핵심 개념

능력 밀도(Capacity Density)

본 논문에서 제안하는 능력 밀도 ρρ는 다음 수식으로 정의됩니다:

ρ=SeffSactualρ=SactualSeff

여기서 SeffSeff는 특정 벤치마크에서 목표 모델과 동등한 성능을 달성하기 위해 필요한 기준 모델(reference model)의 파라미터 크기이며, SactualSactual은 실제 모델 크기입니다. 예를 들어 14B 모델이 70B 기준 모델과 동등한 성능을 보인다면 ρ=5ρ=5가 됩니다.

유효 파라미터 크기(Effective Parameter Size)

기준 모델군(예: LLaMA 시리즈)의 스케일링 법칙을 활용해 성능 예측 모델을 구축합니다. 목표 모델의 다운스트림 태스크 성능을 기준 모델의 성능-크기 곡선에 투영함으로써 SeffSeff를 도출합니다3. 

이 접근법은 서로 다른 아키텍처(예: MoE vs Dense) 간 객관적 비교를 가능케 합니다.

주요 내용

밀도화 법칙(Densing Law)

2021-2024년 오픈소스 기반 모델(LLaMA, Mistral, Qwen 시리즈)을 분석한 결과, 능력 밀도 ρρ가 약 3개월마다 2배씩 지수적으로 성장하는 경향을 확인했습니다3. 구체적인 수치로는:

• 2023년 1월: ρ=1ρ=1 (기준점)
• 2024년 12월: ρ=16ρ=16
  이는 2025년 8월 경 14B 모델이 DeepSeek-R1(2024년 70B급 모델)을 능가할 것임을 시사합니다2.

모델 역량의 시간에 따른 상대적 변화

특정 시점 tt에서의 모델 능력 C(t)C(t)은 다음 식으로 모델링됩니다:

C(t)=C0×2(t−t0)/τC(t)=C0×2(t−t0)/τ

여기서 τ≈3.3τ≈3.3개월이며, C0C0는 초기 능력 밀도입니다. 이에 따르면 2026년 출시 예정인 14B 모델은 2024년 224B 모델에 필적할 것으로 예측됩니다.

시사점

하드웨어 수명 주기 관리

개인용 장비(예: 64GB RAM 탑재 M4 Pro Mac Mini)의 경우, 3년 사용 기간 동안 동일한 파라미터 크기의 모델이 256배(236/3.3236/3.3) 성능 향상을 제공할 수 있습니다. 이는 사용자가 주기적인 하드웨어 업그레이드 없이도 지속적인 성능 개선을 누릴 수 있음을 의미합니다.

 

결론

능력 밀도 개념은 LLM 개발 패러다임을 규모 확장에서 밀도 개선으로 전환하는 이정표입니다. 본 연구가 제시한 밀도화 법칙이 지속된다면, 2027년경에는 1B 미만 모델이 현재 14B 모델 수준의 성능을 제공할 것으로 전망됩니다. 이는 에지 컴퓨팅 장비에서 고성능 AI 서비스 보편화를 가능케 할 기술적 기반이 될 것입니다. 향후 연구과제로는 밀도 증가의 물리적 한계 분석과 양자화 기법(6bit 이하)과의 시너지 효과 규명이 필요할 것으로 보입니다.